Today I am going to talk about the classic Y node problem and P node problems. Then I will show you how we can approach the problem in variety of ways.
Solution 1:
If we know the length of the cycle then we can easily find the node where the cycle starts.
Let C be the length of the cycle.
Take 2 pointers.
One is pointing to the head of the list and the other is pointing to a node C links away from the head.
Advance both the pointers simultaneously.
Both pointers will meet after some time and they will be pointing to the node where the cycle starts.
To find the cycle length:
Take 2 pointers both pointing to the head of the list.
Advance 1 pointer 1 node at a time and the next pointer 2 nodes at a time. (ie one pointer is moving twice as fast as the other one). After sometime they will meet if there is a cycle in the list.
Now stop one pointer.
Start a counter.
Advance the next pointer one node at a time and increment the counter each time till they again meet.
The counter will give us the length of the cycle.
Solution 2:
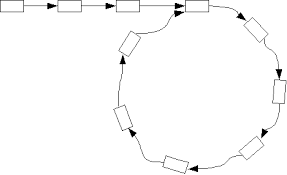
Let C be the length of the cycle and L be the distance from the head to the node where the cycle starts.
In the above figure C = 7 and L = 3.
- Take 2 pointers p1 and p2 both pointing at the head of the list.
- Traverse the list moving p1 at one node at a time and p2 at two nodes at a time.
- If there is a cycle they will definitely meet. Say they meet at a node X distance from the head.
Following are the observations.
- pointer p1 never makes one complete cycle because p2 is faster than p1. (proving is left as an exercise)
- pointer p2 makes atleast 1 cycle.
Let p2 makes N cycles.
Hypothesis:
If we take p1 at the start of the node and p2 at the meeting point and make them travel at the same speed, they will meet where the cycle starts.
Proof:
distance traveled by p1 = X
distance traveled by p2 = X + N*C and N>=1
since p2 has traveled 2 times the distance of p1
Let X = L + d
2 * X = X + N*C
or, X = N*C
or L+d = N*C
or L = (C-d) + (N-1) * C
What conclusion we can draw from this equation?
- From the meeting point of the nodes there are (C-d) nodes remaining to reach the start of the cycle.
Now, if we take p1 at the head of the list and p2 at the meeting point and start traversing both pointers at the same speed:
when p1 travels L distance
p2 travels (C-d) + some number of cycles.
Since travelling the whole cycle doesn't change position, effectively p2 travels (C-d) distance.
Hence they both meet at the start of the cycle.
Solution 3:
- Take 2 pointers p1 and p2 both pointing at the head of the list.
- Traverse the list moving p1 at one node at a time and p2 at two nodes at a time.
- If there is a cycle they will definitely meet. Say they meet at a node X distance from the head.
Let C be the length of the cycle and L be the distance from the head to the node where the cycle starts.
Same definition as above.
After reversing the distance travelled
D = L + C + L
or, L = (D-C)/2
To find C we can use 2 pointer method as above.
Hence from the above information, we can get L.
Hence the result.
To get back the linked list, reverse the list again.
Y-node problem
Given 2 singly Linked List. How can we find a node that is common to both?
A singly linked list has only 1 next pointer. Hence there may be 2 different heads but if the linked list intersect then they will have only 1 tail. ( Y like structure will be formed ).
Hence the Y node problem.
Solution:
Traverse list 1 and let its length be l1
Traverse list 2 and let its length be l2
Take 2 node pointers pointing to the head of the lists.
Traverse abs(l1-l2) distance on the bigger list using the above pointer.
Now move forward both the list pointers until they are equal or the list end had arrived.
if we get both pointers equal at some time, we have the common node.
Easy wasn't it?
This method traverses the list 2 times.
Sometimes traversal may be very costly in real world scenario. In that case we can use Hash/Map to solve it. Left as an exercise for the reader.
P-node Problem
This is a very important problem and is somewhat more complex than the Y-node problem.
Here I will describe 5 methods to solve the P-node problem. Yes, FIVE different methods.
Problem statement:
Given a singly linked list such that it is forming a cycle. We need to find the point where the cycle starts.
Solution 1:
If we know the length of the cycle then we can easily find the node where the cycle starts.
Let C be the length of the cycle.
Take 2 pointers.
One is pointing to the head of the list and the other is pointing to a node C links away from the head.
Advance both the pointers simultaneously.
Both pointers will meet after some time and they will be pointing to the node where the cycle starts.
To find the cycle length:
Take 2 pointers both pointing to the head of the list.
Advance 1 pointer 1 node at a time and the next pointer 2 nodes at a time. (ie one pointer is moving twice as fast as the other one). After sometime they will meet if there is a cycle in the list.
Now stop one pointer.
Start a counter.
Advance the next pointer one node at a time and increment the counter each time till they again meet.
The counter will give us the length of the cycle.
Solution 2:
Let C be the length of the cycle and L be the distance from the head to the node where the cycle starts.
In the above figure C = 7 and L = 3.
- Take 2 pointers p1 and p2 both pointing at the head of the list.
- Traverse the list moving p1 at one node at a time and p2 at two nodes at a time.
- If there is a cycle they will definitely meet. Say they meet at a node X distance from the head.
Following are the observations.
- pointer p1 never makes one complete cycle because p2 is faster than p1. (proving is left as an exercise)
- pointer p2 makes atleast 1 cycle.
Let p2 makes N cycles.
Hypothesis:
If we take p1 at the start of the node and p2 at the meeting point and make them travel at the same speed, they will meet where the cycle starts.
Proof:
distance traveled by p1 = X
distance traveled by p2 = X + N*C and N>=1
since p2 has traveled 2 times the distance of p1
Let X = L + d
2 * X = X + N*C
or, X = N*C
or L+d = N*C
or L = (C-d) + (N-1) * C
What conclusion we can draw from this equation?
- From the meeting point of the nodes there are (C-d) nodes remaining to reach the start of the cycle.
Now, if we take p1 at the head of the list and p2 at the meeting point and start traversing both pointers at the same speed:
when p1 travels L distance
p2 travels (C-d) + some number of cycles.
Since travelling the whole cycle doesn't change position, effectively p2 travels (C-d) distance.
Hence they both meet at the start of the cycle.
Solution 3:
- Take 2 pointers p1 and p2 both pointing at the head of the list.
- Traverse the list moving p1 at one node at a time and p2 at two nodes at a time.
- If there is a cycle they will definitely meet. Say they meet at a node X distance from the head.
- At the meeting point, break the list into 2 parts by removing an edge. (one of them becomes a head and other becomes the tail of the list.
This transforms the problem to the classic Y node problem with 2 head, one at the original head position of the list and the other head which was created after breaking the cycle.
The common node of the lists is the required answer.
We can get back our original list by joining the tail of the list with the second head.
Solution 4:
Reversing a linked list is a very simple problem. Same code will work for a list with cycle too.
A minute thing to observe here is that after reversing the list we finish at the head of the list since a list with cycle has no tail.
Same definition as above.
After reversing the distance travelled
D = L + C + L
or, L = (D-C)/2
To find C we can use 2 pointer method as above.
Hence from the above information, we can get L.
Hence the result.
To get back the linked list, reverse the list again.
Solution 5:
This solution is based on a very important observation about computers.
A pointer is always 4 bytes. (Even char *)
And a structure pointer with more that one members, will always have some trailing zeros. This is due to memory alignment.
Hence we can make use of the trailing zeros to store the visited flag of the node.
To get back the original is a trivial problem.
Awesome post sir
ReplyDeleteGood Post.. I am coming to this website 2nd time, bcoz I saw your soln long time back and I forgot.. While visiting 2nd time, I felt more good...
ReplyDeleteThanks for such post...